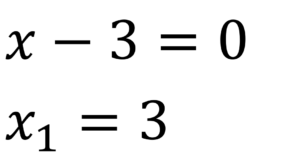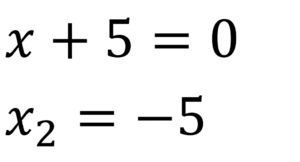ECUACIONES CUADRÁTICAS COMPLETAS
ECUACIONES CUADRÁTICAS COMPLETAS DE LA FORMA ax² + bx + c = 0
Las ecuaciones cuadráticas incompletas son de la forma x² + bx + c = 0 y de la forma ax² + bx + c = 0, donde a es diferente de cero, y están compuestas por tres términos el término cuadrático lineal y el independiente.
Las ecuaciones cuadráticas de la forma x² +bx +c = 0 y de la forma ax² + bx + c = 0 se resuelven de dos formas o métodos más comunes:
métodos más comunes:
- Método de factorización.
- Fórmula General
MÉTODO DE FACTORIZACIÓN
Pasos que debes seguir:
Paso 1. Ordenar la ecuación cuadrática de forma descendente con respecto al exponente de la variable e igualar la ecuación a cero.
Paso 2. Descomponer el polinomio del lado izquierdo del signo igual en dos factores. Para completar los dos factores sigue estos pasos:
a) Calcular la raíz cuadra del término cuadrático y escribir la raíz o resultado en cada factor como primer término.
b) En el primer factor escribes el signo del segundo término de la ecuación, y para el signo del segundo factor multiplicas el signo del segundo término por el signo del tercer término.
c) Busca dos números que multiplicados te de como resultado el tercer término y que sumados o restados obtengas el coeficiente del segundo término. Cuando tienes signos diferentes en tus factores observa bien como debes ubicar los números, es decir que en este paso debes tomar en cuenta la regla número uno de los signos.
Paso 3. Igualar cada factor a cero, es decir se aplica la propiedad del producto cero y despejas la variable en cada ecuación lineal.
Paso 4. Comprueba la ecuación.
Ejemplos resueltos paso por paso
Ejemplo 1. Resolver la siguiente ecuación cuadrática completa.
![]()
Paso 1.
![]()
Paso 2.
![]()
Paso 3.
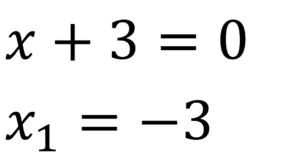
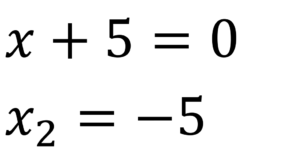
Paso 4.

Ejemplo 2. Resolver la siguiente ecuación cuadrática.
![]()
Paso 1.
![]()
Paso 2.
![]()
Paso 3.
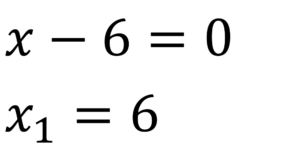
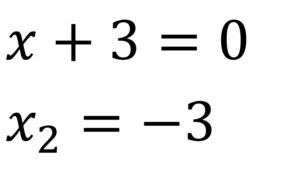
Paso 4.

Ejemplo 3. Resuelve la siguiente ecuación cuadrática.
![]()
Paso 1.
![]()
Paso 2.
![]()
Paso 3.
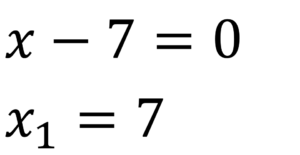
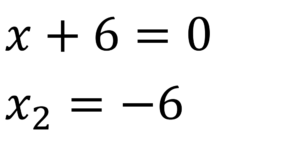
Paso 4.